3.3 Ruler ¶
Our morph ruler is a PlacedMorph6 with a length attribute:
PlacedMorph subclass: #Ruler instanceVariableNames: 'length' classVariableNames: '' poolDictionaries: '' category: 'ArtOfMorph'
Our ruler is to be graduated with metric units, so we define our scale between pixels and centimeters:
ppcm
" pixels per cm " ^ 50.0
To both ease the reading of the graduations and to reveal as much as possible the visuals underneath the ruler, it is painted in a plain color under the markings and with transparency elsewhere.
drawOn: canvas
| font extent |
font := FontFamily familyName: FontFamily defaultFamilyName pointSize: 8.
extent := length * self ppcm + (self ppcm / 2) @ 60.
canvas fillRectangle: (-5 @ 0 corner: extent x @ 25) color: Color yellow.
canvas fillRectangle: (-5 @ 25 corner: extent) color: (Color yellow alpha: 0.5).
canvas frameRectangle: (-5 @ 0 corner: extent) borderWidth: 0.5
color: Color yellow muchDarker.
canvas strokeWidth: 0.8 color: Color black do: [
0 to: length do: [:posX |
canvas moveTo: posX * self ppcm 0.5; lineToY: 10.
canvas moveTo: posX * self ppcm + (self ppcm / 2) @ 0.5; lineToY: 6]].
0 to: length do: [:posX |
canvas drawString: posX asString
atCenterX: posX * self ppcm @ 12 font: font color: Color black]
Figure 3.6: Ruler with a centimeter graduation
When drawing, the coordinates we are using are always considered as part of a coordinate system local to the morph we are drawing into. This makes the task both simple and powerful, and we will be able to benefit from this feature to implement smart user interactions. In the method above, the zero on the ruler coincides with the origin in the morph’s coordinate system.
The drawOn: method above is written to be compact and easy to read; however, the method ppcm is used extensively to convert between centimeters and pixels, which implies numerous multiplications and some divisions. These operations are more expensive than additions. Rewrite drawOn: to avoid multiplication and division, particularly in loops.
Exercise 3.3: Avoid expensive calculus
Exercise 3.4: Millimeter graduation
Figure 3.7: Ruler with a millimeter graduation
You may have noticed that the ruler can be dragged around. When activating its halo of handles – Alt-click or middle-click – it rotates with the blue handle at its bottom-left position.
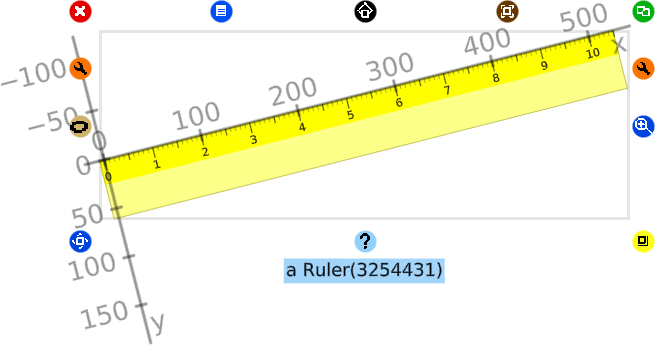
Figure 3.8: Rotating the ruler with its handle
As you’ll experience, it is rotated around the center of its bounding box. From the ruler inspector, ask the ruler about its center:
self rotationCenter ⇒ 260.9997510912408 @ 29.999971389797793
These coordinates are relative – as always in the Cuis-Smalltalk system – to the ruler’s own coordinate system. When pivoting the ruler, it will be more practical if it rotates around its origin; this will make it easier to take measurements on the screen. Fortunately, it is easy to adjust it:
Ruler >> rotationCenter
^ `0@0`
It now rotates around this point!
Using the halo handle to rotate the ruler is not very practical; we need a direct handle on the ruler itself to do so. In the next section, you will learn how to compose our morph designed from scratch with additional morphs.